partitionnement, distinction
Nous sommes à présent en mesure d'assurer que la situation particulière qui nous est présentée (8 jetons déposés dans 5 cases) fait déjà partie d'une famille de 495 membres selon les valeurs du nombre de jetons par case, et que si ces jetons sont différents les uns des autres, elle n'offre pas plus d'intérêt que n'importe laquelle des 390624 autres de la famille des possibles a priori.
Que se passe-t-il si on apprend qu'il y en a parmi les jetons certains ayant des couleurs communes avec d'autres ? On va montrer quantitativement de quelle manière la taille de la famille des possibles passe graduellement de s^j à C_{j+s-1,j} à mesure que les identités (différences) disparaissent au profit des tutelles (couleurs communes) (pour une application un peu provoc).
Il faut reprendre le tableau de l'entrée sur le dénombrement et rappeler que seul le calcul l'antépénultième colonne peut prendre en compte des modifications dans la nature des jetons employés.
En toute généralité, les modes envisageables en ce qui concerne les jetons sont au nombre de d(j,j) qu' on peut directement calculer avec d(j,j) = sum( k=0, k=j-1, D_{j-k} d(k,k) ) et d(0,0)=1 avec les notations déjà vues, et pour chacun d'eux, il faut réévaluer pour chacune des entrées-chapitres la valeur de la colonne intitulée par la formule j!/Prod(val!^occ) qui n'est valable que dans le cas purement distingable.
En réalité, le calcul de cette quantité liée à la dégénérescence et qui est en fait une mesure d'entropie, va reprendre l'essence de la formule citée qui dit qu'on fait le bilan entre les permutations possibles parmi j et les permutations possibles parmi les k jetons d'une même case pour chaque case.
Ici, l'entropie n'est pas calculée en une fois mais est la somme des sous-entropies calculées au fur et à mesure d'une procédure visant à passer en revue les cas de figures. On peut mettre en évidence une adéquation entre les nombres de configurations cherchés et les nombres de chemins dans un graphe défini par le passage d'un sommet à un autre par décrémentation :
Ainsi on a par exemple entropy({3,2,1},{1,1,1,1,1,1}) = 60 : on retrouve que y = 60 = b!/Prod(val!^o) = 6!/(3!2!1!) car l'uplet {1,1,1,1,1,1} indique que tous les jetons sont distincts les uns des autres.
De même, on a
entropy({3,2,1},{2,1,1,1,1}) = 38
entropy({3,2,1}, {2,2,1,1}) = 24
entropy({3,2,1}, {3,1,1,1}) = 19
entropy({3,2,1}, {2,2,2}) = 15
entropy({3,2,1}, {1,2,3}) = 12
entropy({3,2,1}, {4,1,1}) = 8
entropy({3,2,1}, {3,3}) = 6
entropy({3,2,1}, {4,2}) = 5
entropy({3,2,1}, {5,1}) = 3
entropy({3,2,1}, {6}) = 1
et on retrouve que 1=6!/6! car l'uplet {6} indique que tous les jetons sont égaux les uns aux autres.
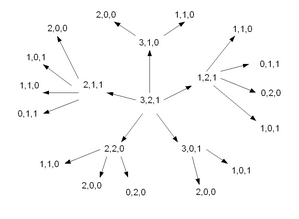
Voici par exemple une illustration correspondant à l'expression entropy({3,2,1},{2,2,2}) = 15, le premier 2 signifiant que l'on définit par 2 le coût de passage de {3,2,1} à la couche 1 suivante (il y a alors 5 cas possibles=5 flèches) et le second 2 définissant également le coût de passage de la couche 1 à la couche 2 (il y a alors 15 de ces façons de passer de {3,2,1} à un upplet de valeur 2). Comme il n'y a qu'une seule manière en enlevant 2 de passer d'un upplet de valeur 2 de la 2ème couche à l'upplet {0,0,0} de valeur nulle, la valeur 15 obtenue à la deuxième couche est donc aussi celle du résultat .
Cette fonction a une intéressante propriété : elle est symétrique ce qui signifie qu'il y a autant de façons de ranger les billes a,b,b,b,c,c,c,c,c dans les boîtes de capacités 2 et 7 dans cet ordre que de façons de ranger les billes d,d,e,e,e,e,e,e,e dans les boîtes de capacités 1,3,5 dans cet ordre.
On peut vérifier qu'en établissant le listing de la manière suivante :
1)toutes lettres identiques rangées selon {3,2,1}:
a,a,a a,a a -> 1 possibilité
2)1 lettre differente, l'ensemble rangé selon {3,2,1}:
a,a,b a,a a
a,a,a a,b a
a,a,a a,a b -> 3 possiblités
3)première configuration à plus de 2 lettres rangées selon {3,2,1}:
.
.
.
11)dernière configuration à plus de 2 lettres : toutes les lettres distinctes les unes des autres rangées selon {3,2,1}:
a,b,c d,e f
.
.
.
f,e,d c,b a -> 60 possibilités,
on retrouve bien en comptabilisant les possibilités les différentes valeurs de la suite obtenue précédemment.
Il est important de noter qu' ici, la suite des d(6,6)=11 valeurs est rangée dans l'ordre croissant en ayant choisi de la générer en prenant pour deuxième argument de la foncton entropy les différentes valeurs non nulles des uplets x rangés dans l'ordre déjà rencontré pour l'implémentation. En fait c'est un cas particulier car si on la note E comme fonction d'un uplet
E({3,2,1}) = (1,3,5,6,8,12,15,19,24,38,60),
alors il existe au moins un u tel que E(u) ne soit pas rangée dans l'ordre croissant alors que les x utilisés sont classés, par exemple E({5,3,1})=(1,3,5,7,8,8,13,17,18,20,24,27,20,31,37,44,49,58,47,67,74,88,104,101,132,156,197,232,343,504).
Que se passe-t-il si on apprend qu'il y en a parmi les jetons certains ayant des couleurs communes avec d'autres ? On va montrer quantitativement de quelle manière la taille de la famille des possibles passe graduellement de s^j à C_{j+s-1,j} à mesure que les identités (différences) disparaissent au profit des tutelles (couleurs communes) (pour une application un peu provoc).
Il faut reprendre le tableau de l'entrée sur le dénombrement et rappeler que seul le calcul l'antépénultième colonne peut prendre en compte des modifications dans la nature des jetons employés.
En toute généralité, les modes envisageables en ce qui concerne les jetons sont au nombre de d(j,j) qu' on peut directement calculer avec d(j,j) = sum( k=0, k=j-1, D_{j-k} d(k,k) ) et d(0,0)=1 avec les notations déjà vues, et pour chacun d'eux, il faut réévaluer pour chacune des entrées-chapitres la valeur de la colonne intitulée par la formule j!/Prod(val!^occ) qui n'est valable que dans le cas purement distingable.
En réalité, le calcul de cette quantité liée à la dégénérescence et qui est en fait une mesure d'entropie, va reprendre l'essence de la formule citée qui dit qu'on fait le bilan entre les permutations possibles parmi j et les permutations possibles parmi les k jetons d'une même case pour chaque case.
Ici, l'entropie n'est pas calculée en une fois mais est la somme des sous-entropies calculées au fur et à mesure d'une procédure visant à passer en revue les cas de figures. On peut mettre en évidence une adéquation entre les nombres de configurations cherchés et les nombres de chemins dans un graphe défini par le passage d'un sommet à un autre par décrémentation :
- Comme l'exemple utilisé jusque là est assez surdimensionné pour ce que je veux souligner, je vais utiliser la petite version du même problème avec b=6 billes dans c=3 cases.
- Parmi les d(6,3)=7 chapitres principaux, on choisit de s'intéresser à celui qui raconte la situation où trois billes sont dans une case , deux dans une autre et la dernière dans la dernière c'est-à-dire {3,2,1}.
- D'une part, on peut tracer le graphe en plaçant le sommet {3,2,1} au centre et en traçant les arètes à partir de lui vers ce qu'il est possible d'atteindre en otant 1 à la première, la seconde ou la troisième valeur de ce sommet : {2,2,1}, {3,1,1} et {3,2,0} c'est-à-dire 3 valeurs. On peut faire de même en otant 2 et on obtient:{2,2,0}, {2,1,1}, {3,0,1}, {1,2,1}, {3,1,0} c'est-à-dire 5 valeurs...
- D'autre part, on peut tracer manuellement les d(6,6)=11 configurations possibles pour l'agencement des différences entre jetons et mesurer l'effet de chacun sur l'entropie liée à {3,2,1}
Ainsi on a par exemple entropy({3,2,1},{1,1,1,1,1,1}) = 60 : on retrouve que y = 60 = b!/Prod(val!^o) = 6!/(3!2!1!) car l'uplet {1,1,1,1,1,1} indique que tous les jetons sont distincts les uns des autres.
De même, on a
entropy({3,2,1},{2,1,1,1,1}) = 38
entropy({3,2,1}, {2,2,1,1}) = 24
entropy({3,2,1}, {3,1,1,1}) = 19
entropy({3,2,1}, {2,2,2}) = 15
entropy({3,2,1}, {1,2,3}) = 12
entropy({3,2,1}, {4,1,1}) = 8
entropy({3,2,1}, {3,3}) = 6
entropy({3,2,1}, {4,2}) = 5
entropy({3,2,1}, {5,1}) = 3
entropy({3,2,1}, {6}) = 1
et on retrouve que 1=6!/6! car l'uplet {6} indique que tous les jetons sont égaux les uns aux autres.
Voici par exemple une illustration correspondant à l'expression entropy({3,2,1},{2,2,2}) = 15, le premier 2 signifiant que l'on définit par 2 le coût de passage de {3,2,1} à la couche 1 suivante (il y a alors 5 cas possibles=5 flèches) et le second 2 définissant également le coût de passage de la couche 1 à la couche 2 (il y a alors 15 de ces façons de passer de {3,2,1} à un upplet de valeur 2). Comme il n'y a qu'une seule manière en enlevant 2 de passer d'un upplet de valeur 2 de la 2ème couche à l'upplet {0,0,0} de valeur nulle, la valeur 15 obtenue à la deuxième couche est donc aussi celle du résultat .

Cette fonction a une intéressante propriété : elle est symétrique ce qui signifie qu'il y a autant de façons de ranger les billes a,b,b,b,c,c,c,c,c dans les boîtes de capacités 2 et 7 dans cet ordre que de façons de ranger les billes d,d,e,e,e,e,e,e,e dans les boîtes de capacités 1,3,5 dans cet ordre.
On peut vérifier qu'en établissant le listing de la manière suivante :
1)toutes lettres identiques rangées selon {3,2,1}:
a,a,a a,a a -> 1 possibilité
2)1 lettre differente, l'ensemble rangé selon {3,2,1}:
a,a,b a,a a
a,a,a a,b a
a,a,a a,a b -> 3 possiblités
3)première configuration à plus de 2 lettres rangées selon {3,2,1}:
.
.
.
11)dernière configuration à plus de 2 lettres : toutes les lettres distinctes les unes des autres rangées selon {3,2,1}:
a,b,c d,e f
.
.
.
f,e,d c,b a -> 60 possibilités,
on retrouve bien en comptabilisant les possibilités les différentes valeurs de la suite obtenue précédemment.
Il est important de noter qu' ici, la suite des d(6,6)=11 valeurs est rangée dans l'ordre croissant en ayant choisi de la générer en prenant pour deuxième argument de la foncton entropy les différentes valeurs non nulles des uplets x rangés dans l'ordre déjà rencontré pour l'implémentation. En fait c'est un cas particulier car si on la note E comme fonction d'un uplet
E({3,2,1}) = (1,3,5,6,8,12,15,19,24,38,60),
alors il existe au moins un u tel que E(u) ne soit pas rangée dans l'ordre croissant alors que les x utilisés sont classés, par exemple E({5,3,1})=(1,3,5,7,8,8,13,17,18,20,24,27,20,31,37,44,49,58,47,67,74,88,104,101,132,156,197,232,343,504).
